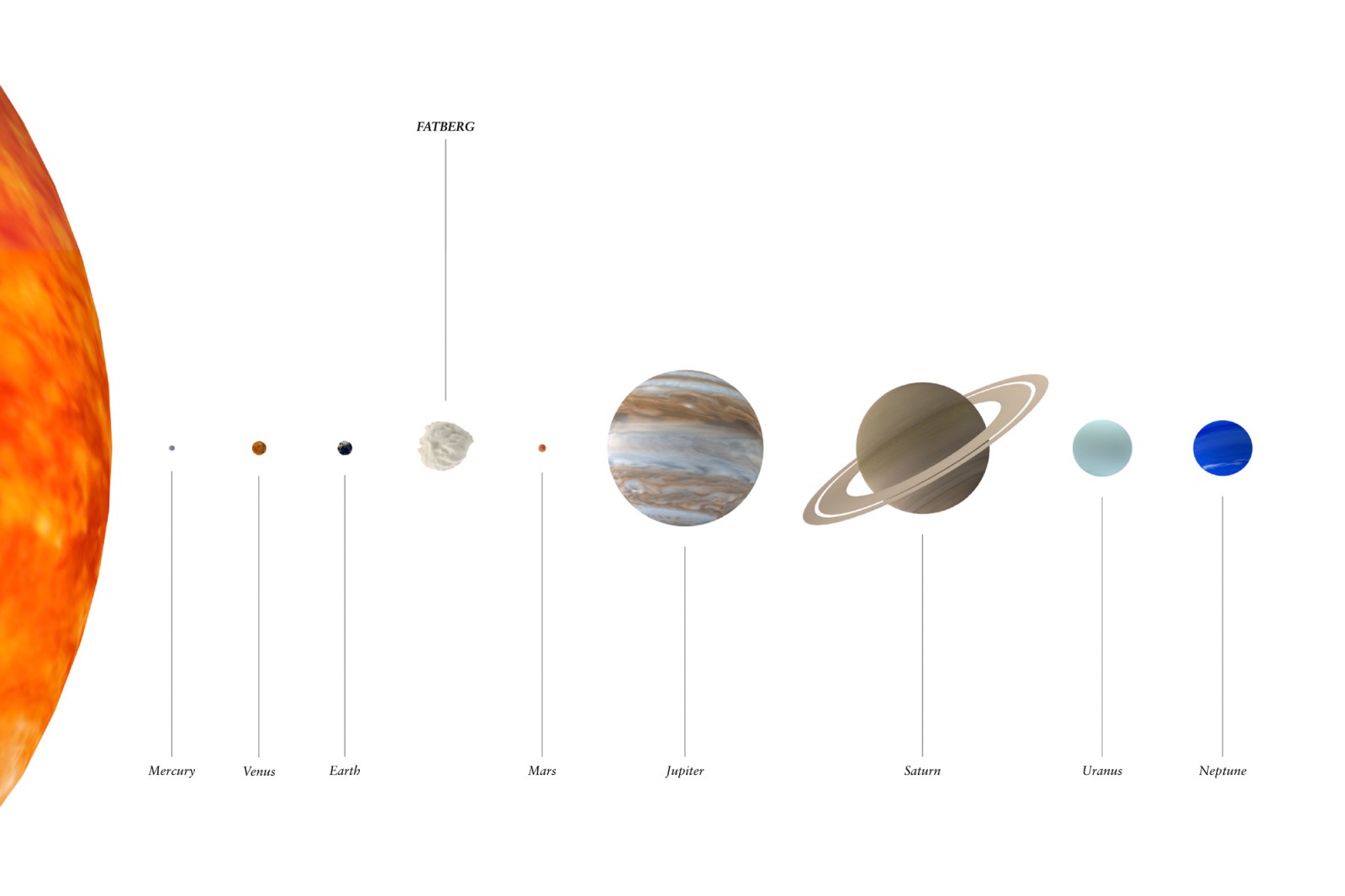
If we used all the hydrogen, oxygen or carbon on Earth to make fat, how big a FATBERG could we build? We put this question to Alex Motta, molecular biologist and founder of 010SciArt.

First we needed to choose which fat to use in the calculation. There are many different kinds of fat, some simpler and with fewer molecules than others. A triglyceride is the molecular form in which fatty acids are stored. They are composed of one molecule of glycerol, on which there are 3 branched molecules of fatty acids. For this calculation we opted for an average triglyceride – the triglyceride most present in lard (1,3-Dioleoyl-2-palmitoylglycerol). This particular fat has a molecular weight of 859.39 grams per mole*, and a density of 0.919. It has 55 atoms of carbon, 6 atoms of oxygen and A LOT of hydrogen.

There are 1.33×10^50 atoms on earth and the relative abundance of oxygen, hydrogen and carbon atoms are (in parts per billion) 482,000,000, 6,700,000 and 1,600,000 respectively. These proportions do not reflect those found in our fat triglyceride, so one of these elements must be selected to base our calculations on. We selected oxygen for its crucial role in the appearance and maintenance of life on Earth. Bearing this in mind, if we divide the total amount of oxygen atoms on Earth by 6, the total number of lard triglycerides that can be made with all the oxygen atoms on Earth is 1.06843×10^49 molecules. This means the Maximum FATBERG would have a mass of 1.52×10^28 grams, and a volume of 1.66×10^22 m3. If you compare this to Earth, with its volume of 1.1×10^21 m3, this means that the Maximum FATBERG would be approximately 15 times the volume of Earth.

The calculation above should be regarded as a conceptual exercise and a first attempt to explore the full potential of fat – something we aim to explore further in the coming months.

*A mole is the system of physical units of an amount of substance, equal to the quantity containing as many elementary units as there are atoms in 0.012 kg of carbon-12.

Initial research and rendering by Santini Basra
Calculations by Alex Motta (010SciArt)